Задачи по ТОЭ: примеры решения задач по теоретическим основам электротехники

Формулы, примеры решения задач: ТОЭ | Электрические машины | Высшая математика | Теоретическая механика

Решение примеров по ТОЭ

Примеры решения задач по ТОЭ

Электрические цепи постоянного тока ➠
Электрические цепи переменного тока ➠
Трехфазные цепи ➠
Переходные процессы в линейных электрических цепях ➠
Периодические синусоидальные токи в электрических цепях ➠
Электромагнитные устройства ➠
Электрические измерения и приборы ➠
Трансформаторы ➠
Машины постоянного тока ➠
Асинхронные машины ➠
Синхронные машины ➠
Источник: «Кафедра ФН7» МГТУ им. Баумана

Пример 1. Первый закон Кирхгофа.
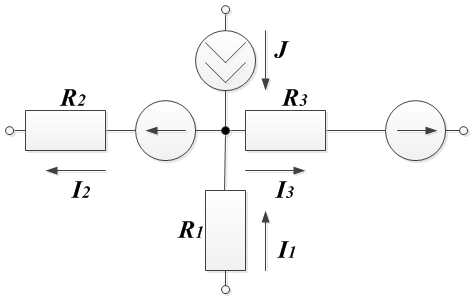
Пример 1. Рисунок к первому закону Кирхгофа
Для схемы составить уравнение по первому закону Кирхгофа.

Решение:
По первому закону Кирхгофа алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю.

Токи, направленные к узлу, берем со знаком плюс, а токи, направленные от узла, берем со знаком минус.

В итоге запишем уравнение первого закона Кирхгофа, применительно к данной схеме:
J+I_1-I_2-I_3=0 .

Ответ: J+I_1-I_2-I_3=0 .

Пример 2. Второй закон Кирхгофа.
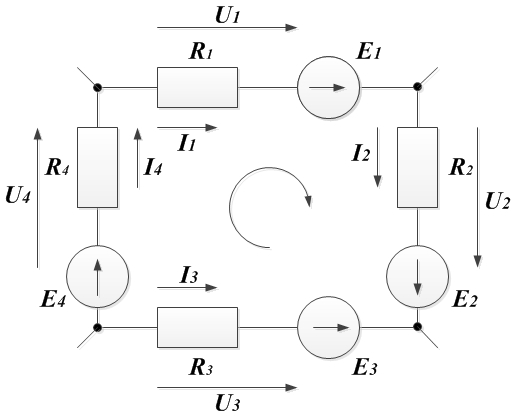
Пример 2. Рисунок ко второму закону Кирхгофа
Для изображенного на рисунке контура составить уравнение по второму закону Кирхгофа.

Решение:
Второй закон Кирхгофа: алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура $sum{k=1}{n}{{I_k}{R_k}}=sum{p=1}{m}{E_p}$ . Или
Алгебраическая сумма напряжений вдоль любого замкнутого контура равна нулю:
$sum{k=1}{n}{U_k}=0$ .

При расчете электрической цепи число неизвестных токов равно числу ветвей в цепи p. По второму закону Кирхгофа составляется k=p-q+1 уравнений.

При определении числа ветвей (p) не учитывают ветви с R = 0, а ветви с одним и тем же током принимают за одну ветвь. При определении числа узлов (q) учитывают только те узлы, в которых сходится более чем две ветви, а ветви с R = 0 включают в состав узла.

В каждом контуре произвольно выбирают направление обхода контура.
Напряжения и ЭДС в уравнении берут с положительным знаком, если направление напряжений, ЭДС и токов совпадает с направлением обхода контура.

Выбираем направление обхода контура по часовой стрелке. Запишем для нашего контура уравнения по второму закону Кирхгофа:
I_1*R_1+I_2*R_2-I_3*R_3+I_4*R_4=E_1+E_2-E_3+E_4 , или
U_1+U_2-U_3+U_4=0 .

Ответ: I_1*R_1+I_2*R_2-I_3*R_3+I_4*R_4=E_1+E_2-E_3+E_4 , или U_1+U_2-U_3+U_4=0 .

Пример 3. Метод контурных токов.
Пример 3. Рисунок к методу контурных токов
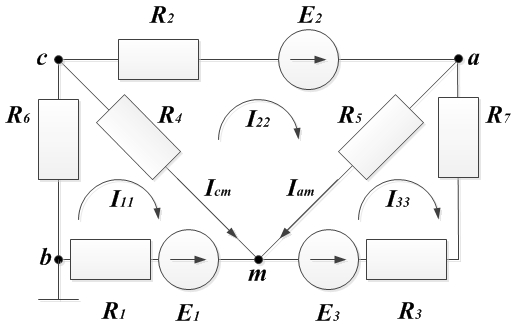
Дано:
R₁ = 4 Ом; R₂ = 10 Ом; R₃ = 1 Ом; R₄ = 5 Ом; R₅ = 2 Ом; R₆ = 5 Ом; R₇ = 2 Ом; E₁ = 10 В; E₂ = 10 В; E₃ = 8 В;
Найти:
Токи в схеме методом контурных токов.
I₁₁, I₂₂, I₃₃, I_am, I_cm — ?

Решение:
Выберем направления всех контурных токов по часовой стрелке.
Положим, что в левом контуре по часовой стрелке течет контурный ток I₁₁, в верхнем (также по часовой стрелке) — контурный ток I₂₂, в правом (также по часовой стрелке) — контурный ток I₃₃.

Для каждого контура составим уравнения по второму закону Кирхгофа. При этом учтем, что по ветви cm (с сопротивлением R₄) течет сверху вниз ток I_cm равный I_11-I_22 , а по ветви am (с сопротивлением R₅) течет сверху вниз ток I_am равный I_22-I_33 .
Направления обхода контуров примем также по часовой стрелке.

Определяем полное сопротивление первого контура:
R_11=R_1+R_6+R_4=4+5+5=14 Ом.

Определяем полное сопротивление второго контура:
R_22=R_2+R_5+R_4=10+2+5=17 Ом.

Определяем полное сопротивление третьего контура:
R_33=R_3+R_5+R_7=1+2+2=5 Ом.

Сопротивление смежной ветви между контурами входит в уравнение со знаком минус, если направления контурных токов вдоль этой ветви встречны, и со знаком плюс, если направления этих токов согласны.

Сопротивление смежной ветви первого и второго контура:
R_12=R_21=-R_4=-5 Ом.

Сопротивление смежной ветви первого и третьего контура:
R_13=R_31=0 Ом.

Контурная ЭДС первого контура, равна алгебраической сумме ЭДС этого контура (в нее со знаком плюс входят те ЭДС, направления которых совпадают с направлением обхода контура):
E_11=-E_1=-10 В.

Контурная ЭДС второго контура:
E_22=E_2=10 В.

Контурная ЭДС третьего контура:
E_33=-E_3=-8 В.

Применив второй закон Кирхгофа, составим систему уравнений для трех контуров в общем виде:
$delim{}{matrix{3}{7}{{R_{11}I_11} {+} {R_{12}I_22} {+} {R_{13}I_33} {=} {E_11,~} {R_{21}I_11} {+} {R_{22}I_22} {+} {R_{23}I_33} {=} {E_22,~} {R_{31}I_11} {+} {R_{32}I_22} {+} {R_{33}I_33} {=} {E_33,~}}}{rbrace}$

или в матричной форме (R)*(I)=(E) ;

$(matrix{3}{3}{{R_{11}} {R_{12}} {R_{13}} {R_{21}} {R_{22}} {R_{23}} {R_{31}} {R_{32}} {R_{33}}})*(matrix{3}{1}{{I_{11}} {I_{22}} {I_{33}}})*(matrix{3}{1}{{E_{11}} {E_{22}} {E_{33}}})$ .

Подставим в систему уравнений численные значения:
$delim{}{matrix{3}{7}{{14I_11} {-} {5I_22} {+} {0I_33} {=} {-10,~} {-5I_11} {+} {17I_22} {-} {2I_33} {=} {10,~} {0I_11} {-} {2I_22} {+} {5I_33} {=} {-8.~}}}{rbrace}$

Вычислим главный определитель системы применив «правило треугольников»:
{Delta}=delim{|}{matrix{3}{3}{{14} {-5} {0} {-5} {17} {-2} {0} {-2} {5}} }{|}=14*17*5+(-5)*(-2)*0+0*(-5)*(-2)-
{-}0*17*0-(-2)*(-2)*14-5*(-5)*(-5)=1009 .

Операции с матрицами, решение систем линейных уравнений, нахождение определителя с этими вычислениями качественно и быстро справляется он-лайн калькулятор, использованный при решении задачи 4.

Главный определитель системы линейных уравнений не равен нулю, значит система совместна и определена. Используя формулы Крамера, находим единственное решение уравнений: $I_11={{Delta}_1}/{Delta},~I_22={{Delta}_2}/{Delta},~I_33={{Delta}_3}/{Delta},$
где Δ₁ — определитель, получаемый из главного определителя системы Δ заменой первого столбца на столбец свободных членов (столбец матрицы E);
Δ₂ — определитель, получаемый из главного определителя системы Δ заменой второго столбца на столбец свободных членов (столбец матрицы E);
Δ₃ — определитель, получаемый из главного определителя системы Δ заменой третьего столбца на столбец свободных членов (столбец матрицы E).

Вычисляем контурные токи:
$I_11={delim{|}{matrix{3}{3}{{-10} {-5} {0} {10} {17} {-2} {-8} {-2} {5}} }{|}}/{1009}=$ {=}{-10*17*5+(-5)*(-2)*(-8)+0*10*(-2)-(-8)*17*0-(-2)*(-2)*(-10)-5*10*(-5)}/1009=
{=}-640/1009=-0,634~A ;

$I_22={delim{|}{matrix{3}{3}{{14} {-10} {0} {-5} {10} {-2} {0} {-8} {5}} }{|}}/{1009}=$ {=}{14*10*5+(-10)*(-2)*0+0*(-5)*(-8)-0*10*0-(-8)*(-2)*14-5*(-5)*(-10)}/1009=
{=}226/1009=0,224~A ;

$I_33={delim{|}{matrix{3}{3}{{14} {-5} {-10} {-5} {17} {10} {0} {-2} {-8}} }{|}}/{1009}=$ {=}{14*17*(-8)+(-5)*10*0+(-10)*(-5)*(-2)-0*17*(-10)-(-2)*10*14-(-8)*(-5)*(-5)}/1009=
{=}-1524/1009=-1,51~A .

Определяем токи в смежных ветвях:
$I_{cm}=I_11-I_22=-0,634-0,224=-0,858~A$ ;
$I_{am}=I_22-I_33=0,224-(-1,51)=1,734~A$ .

Ответ: $I_{11}=-0,634~A;~I_{22}=0,224~A;~I_{33}=-1,51~A;~I_{cm}=-0,858~A;~I_{am}=-1,734~A.$

Пример 4. Метод узловых потенциалов.
Пример 4. Рисунок к методу узловых потенциалов
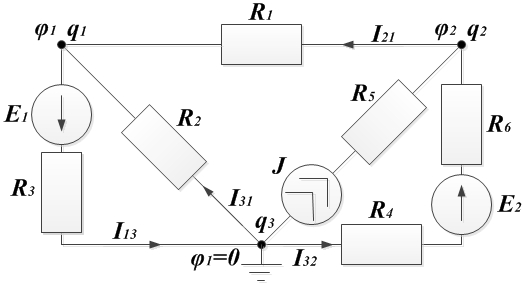
Дано:
R₁ = 5 Ом; R₂ = 10 Ом; R₃ = 10 Ом; R₄ = 3 Ом; R₅ = 40 Ом; R₆ = 7 Ом; E₁ = 40 В; E₂ = 10 В; J = 1 А.
Найти:
Токи в схеме методом узловых потенциалов.
I₁₃, I₃₁, I₂₁, I₃₂, — ?

Решение:

Общее число ветвей схемы равно 5.

Число ветвей схемы с источниками тока равно 1.

Число ветвей схемы с неизвестными токами равно 4.

Число узлов схемы 3, нумеруем их, при этом один (q₃), произвольно выбранный, заземляем. Его потенциал принимается равным нулю (ϕ₃=0).

Выбираем направления токов в ветвях: в ветвях с ЭДС – согласно с ней, в остальных ветвях – произвольно. Обозначаем токи двумя индексами: первый – номер узла, от которого ток утекает, второй – номер узла, к которому ток подтекает.

Записываем выражения для токов в ветвях через потенциалы узлов:
$I_13={{varphi}_1-{varphi}_3+E_1}/R_3;~I_21={{varphi}_2-{varphi}_1}/R_1;~I_31={{varphi}_3-{varphi}_1}/R_2;~I_32={{varphi}_3-{varphi}_2+E_2}/{R_4+R_6}.$

Составляем уравнения по первому закону Кирхгофа для тех узлов, потенциалы которых неизвестны (q₁, q₂):
I_31+I_21-I_13=0;
-I_21+I_32+J=0.

В уравнениях заменяем токи в ветвях выражениями для токов в ветвях через потенциалы узлов:
${{varphi}_3-{varphi}_1}/R_2+{{varphi}_2-{varphi}_1}/R_1-{{varphi}_1-{varphi}_3+E_1}/R_3=0;$
$-{{varphi}_2-{varphi}_1}/R_1+{{varphi}_3-{varphi}_2+E_2}/{R_4+R_6}+J=0.$

Подставив в уравнения данные известных величин, получаем следующую систему уравнений:
$delim{}{matrix{2}{7}{{{0-{varphi}_1}/10} {+} {{{varphi}_2-{varphi}_1}/5} {-} {{{varphi}_1-{varphi}_3+40}/10} {=} {0;~} {-{{varphi}_2-{varphi}_1}/5} {+} {{{varphi}_3-{varphi}_2+10}/{3+7}} {+} {1} {=} {0.~}}}{rbrace}$

Умножив все члены уравнений на 10, после необходимых преобразований получаем удобную для расчетов систему уравнений:
$delim{}{matrix{2}{5}{{-4{varphi}_1} {+} {2{varphi}_2} {=} {40;~} {2{varphi}_1} {-} {3{varphi}_2} {=} {-20.~}}}{rbrace}$

Применив метод Крамера, метод Гауcса, метод обратной матрицы или воспользовавшись матричным он-лайн калькулятором, решаем систему уравнений.
В итоге, получаем ${varphi}_1=-10~B;~{varphi}_2=0~B.$

Найденные значения потенциалов подставляем в формулы и находим, таким образом, искомые токи ветвей:
$I_13=I_1={{varphi}_1-{varphi}_3+E_1}/R_3={-10-0+40}/10=3~A;$
$I_21=I_3={{varphi}_2-{varphi}_1}/R_1={0-(-10)}/5=2~A;$
$I_31=I_2={{varphi}_3-{varphi}_1}/R_2={0-(-10)}/10=1~A;$
$I_32=I_4={{varphi}_3-{varphi}_2+E_2}/{R_4+R_6}={0-0+10}/{3+7}=1~A.$

Второй вариант решения задачи.

Общее число ветвей схемы равно шести.

Схема содержит одну ветвь с источником тока.

Схема содержит четыре ветви с неизвестными токами.

Число узлов схемы равно трем, нумеруем их, при этом один, произвольно выбранный (q₃), заземляем. Его потенциал принимаем равным нулю.

Произвольно выбираем направления токов в ветвях.

Определяем проводимость ветвей, сходящихся в узле q₁:
G_11=1/R_1+1/R_2+1/R_3=1/5+1/10+1/10=0,4 См.

Определяем проводимость ветвей, сходящихся в узле q₂:
$G_22=1/R_1+1/{R_4+R_6}=1/5+1/{3+7}=0,3$ См.
Проводимость ветви, содержащей источник тока равна 0, так как сопротивление источника тока равно бесконечности.

Проводимость ветви, непосредственно соединяющей узлы q₁ и q₂ берем со знаком минус:
G_12=G_21=-1/R_1=-1/5=-0,2 См.

Определяем узловые токи:
$I_11=-E_1/R_3=-40/10=-4~A,~I_22=E_2/{R_4+R_6}+J=10/{3+7}+1=2~A.$

Получаем систему уравнений:
$delim{}{matrix{2}{5}{{{(1/R_1+1/R_2+1/R_3)}{varphi}_1} {-} {{1/R_1}{varphi}_2} {=} {-E_1/R_3;~} {-1/R_1{varphi}_1} {+} {{1/R_1+1/{R_4+R_6}}{varphi}_2} {=} {E_2/{R_4+R_6}+J.~}}}{rbrace}$

$delim{}{matrix{2}{5}{{0,4{varphi}_1} {-} {0,2{varphi}_2} {=} {-4;~} {-0,2{varphi}_1} {+} {0,3{varphi}_2} {=} {2.~}}}{rbrace}$

Решаем полученную систему уравнений относительно потенциалов узлов.
В итоге, получаем ${varphi}_1=-10~B;~{varphi}_2=0~B.$

Определяем токи ветвей по закону Ома для участка цепи, содержащего ЭДС:
$I_1={{varphi}_1-{varphi}_3+E_1}/R_3={-10-0+40}/10=3~A;$
$I_3={{varphi}_2-{varphi}_1}/R_1={0-(-10)}/5=2~A;$
$I_2={{varphi}_3-{varphi}_1}/R_2={0-(-10)}/10=1~A;$
$I_4={{varphi}_3-{varphi}_2+E_2}/{R_4+R_6}={0-0+10}/{3+7}=1~A.$

Ответ: I_13=I_1=3~A; I_21=I_3=2~A; I_31=I_2=1~A; I_32=I_4=1~A.

Пример 5. Метод эквивалентного генератора.
Схема к примеру 5. Метод эквивалентного генератора
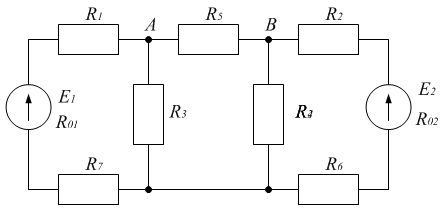
Дано: Е₁ = 200 В; Е₂ = 50 В; R₀₁ = R₀₂ = 0,5 Ом; R₁ = R₂ = 4,5 Ом; R₃ = 5 Ом; R₄ = 10 Ом; R₅ = 1,25 Ом; R₆ = 5 Ом; R₇ = 10 Ом.
Найти: I₅ — ?

Решение:
Для решения примера применяем метод эквивалентного генератора.
Чтобы найти ЭДС эквивалентного генератора, предположим разрыв в ветви с сопротивлением R₅ (так называемый режим холостого хода), значит ток в этой ветви равен 0.
Получаем схему из двух замкнутых контуров с источникам ЭДС Е₁, Е₂:
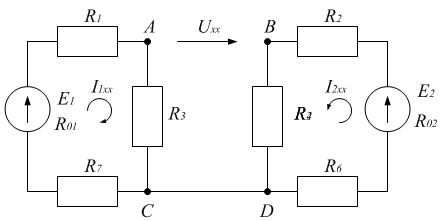
Схема к примеру 5. Режим холостого хода
По закону Ома находим токи в каждом контуре:
$I_{1xx}=E_1/{R_{01}+R_1+R_3+R_7}=200/{0,5+4,5+5+10}=200/20=10~A.$
$I_{2xx}=E_2/{R_{02}+R_6+R_4+R_2}=50/{0,5+5+10+4,5}=50/20=2,5~A.$

Формула для определения напряжения холостого хода:
$U_{xx}={varphi}_A-{varphi}_B.$

Если принять потенциалы точек C и D равными 0: ${varphi}_C={varphi}_D=0$ , тогда потенциалы точек А и В будут выше потенциалов точек С и D на величины потерь напряжений $R_{3}I_{1xx}$ и $R_{4}I_{2xx}$ в ветвях АС и BD:
${varphi}_A={varphi}_C+R_{3}I_{1xx}=0+5*10=50~B;$
${varphi}_B={varphi}_D+R_{4}I_{2xx}=0+10*2,5=25~B.$

Подставив в формулу для определения напряжения холостого хода, значения потенциалов, получим:
$U_{xx}={varphi}_A-{varphi}_B=50-25=25~B$

Если предположить, что ЭДС Е₁ и Е₂ равны нулю, то внутреннее сопротивление эквивалентного генератора равно входному сопротивлению цепи со стороны точек А и В.
Между точками А и С, В и D в этой схеме включены две пары ветвей, которые соединены между собой последовательно.
Значит, можно записать, что
$R_{BX}={R_3*(R_1+R_{01}+R_7)}/{R_3+R_1+R_{01}+R_7}+{R_4*(R_2+R_{02}+R_6)}/{R_4+R_2+R_{02}+R_6}=$
{}={5*(4,5+0,5+10)}/{5+4,5+0,5+10}+{10*(4,5+0,5+5)}/{10+4,5+0,5+5}=75/20+100/20=8,75 Ом.

Применив закон Ома для всей цепи определяем ток I_5 :
$I_5=U_{xx}/{(R_{BX}+R_5)}=25/{(8,75+1,25)}=25/10=2,5~A.$

Ответ: I_5=5~A.

Пример 6. Входное сопротивление. Преобразование звезды в треугольник.
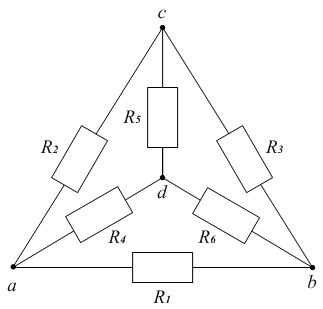
Схема к примеру 6
Дано:
R₁ = 1 Ом; R₂ = 2 Ом; R₃ = 3 Ом; R₄ = 4 Ом; R₅ = 5 Ом; R₆ = 6 Ом.
Найти: R_ab — ?

Решение.
Для определения входного (относительно точек a и b) сопротивления схемы необходимо выполнить ряд преобразований.

Звезду, состоящую из сопротивлений R₄, R₅, R₆, преобразуем в треугольник.

$R_45=R_4+R_5+{R_4*R_5}/R_6=4+5+{4*5}/6=12,3$ Ом;
$R_56=R_5+R_6+{R_5*R_6}/R_4=5+6+{5*6}/4=18,5$ Ом;
$R_46=R_4+R_6+{R_4*R_6}/R_5=4+6+{4*6}/5=14,8$ Ом.

В результате преобразований получаем схему:
Схема к примеру 6. Преобразование звезды в треугольник
Параллельно включенные сопротивления заменяем эквивалентными:
$R_{1-46}={R_{46}*R_1}/{R_{46}+R_1}={14,8*1}/{14,8+1}=0,937$ Ом;
$R_{2-45}={R_{45}*R_2}/{R_{45}+R_2}={12,3*2}/{12,3+2}=1,721$ Ом;
$R_{3-56}={R_{56}*R_3}/{R_{56}+R_3}={18,5*3}/{18,5+3}=2,581$ Ом.

В результате преобразований получаем схему:
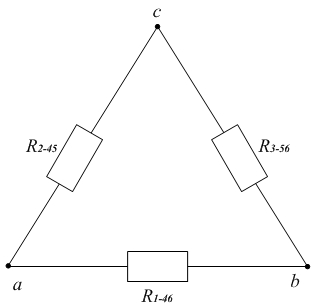
Схема к примеру 6. Параллельное соединение

Определяем входное сопротивление схемы относительно точек a и b:
$R_{ab}={R_{1-46}*(R_{2-45}+R_{3-56})}/{R_{1-46}+R_{2-45}+R_{3-56}}={0,937*(1,721+2,581)}/{0,937+1,721+2,581}=0,769$ Ом.

Ответ: входное сопротивление схемы $R_{ab}=0,769$ Ом.

Задача 1. Вывести формулу для емкости плоского конденсатора
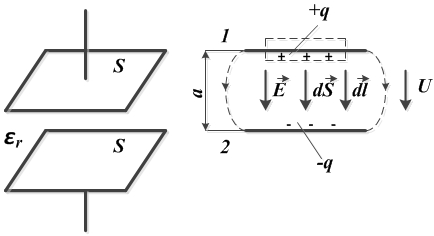
Задача 1. Рисунок 1. Плоский конденсатор
Площадь каждой пластины конденсатора (с одной стороны) S, расстояние между пластинами конденсатора а, относительная диэлектрическая проницаемость диэлектрика ε_r.

Решение:
На виде сбоку показаны силовые линии. В основной области поле однородно. На краях имеется некоторая неоднородность, которую учитывать не будем. vec{E} направлена от заряда +q к заряду –q.

Напряжение между электродами конденсатора:
$U=int{1}{2}{{vec{E}}d{vec{l}}}=int{1}{2}{Ecos0^0{dl}}=Ea$ .

Охватим верхний электрод конденсатора замкнутой поверхностью (на рисунке показан пунктиром) и применим к ней теорему Гаусса:
$oint{}{}{{vec{E}}d{vec{S}}}=ES=q/{{{varepsilon}_0}{{varepsilon}_r}}$ . Значит,
$E=q/{{{varepsilon}_0}{{varepsilon}_r}S}$ , а формула для определения емкости плоского конденсатора примет вид:
$C=q/U={{{varepsilon}_0}{{varepsilon}_r}S}/a$ .

Ответ: $C={{{varepsilon}_0}{{varepsilon}_r}S}/a$ — формула емкости плоского конденсатора.

Задача 2. Вывести формулу емкости цилиндрического конденсатора
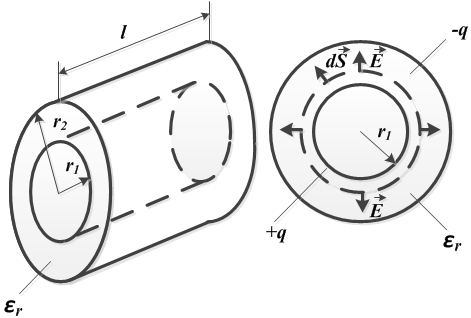
Задача 2. Рисунок 1. Цилиндрический конденсатор
На внутреннем электроде радиусом r₁ находится заряд +q, на наружном электроде радиусом r₂ — заряд –q.

Решение:
Окружим внутренний электрод цилиндрической замкнутой поверхностью радиуса r{r₁ < r < r₂).

Поток вектора vec{E} имеет место через боковую поверхность, через торцы поток отсутствует, так как на торцах d{vec{S}} и vec{E} взаимно перпендикулярны:
$oint{}{}{{vec{E}}d{vec{S}}}={Ecos0^0{dS}}=E2{pi}rl=q/{{{varepsilon}_0}{{varepsilon}_r}}$ . Получаем $E=q/{{2{pi}rl{varepsilon}_0}{{varepsilon}_r}}$

Напряжение между электродами цилиндрического конденсатора:
$U=int{r_1}{r_2}{{vec{E}}d{vec{r}}}=q/{{2{pi}rl{varepsilon}_0}{{varepsilon}_r}}int{r_1}{r_2}{{dr}/r}={q/{{2{pi}rl{varepsilon}_0}{{varepsilon}_r}}}*{ln{{r_2}/{r_1}}}$ .

Получаем формулу для расчета емкости цилиндрического конденсатора:
$C=q/U={{{varepsilon}_0}{{varepsilon}_r}2{pi}}/{ln{{r_2}/{r_1}}}$ .

Ответ: $C={{{varepsilon}_0}{{varepsilon}_r}2{pi}}/{ln{{r_2}/{r_1}}}$ — формула емкости цилиндрического конденсатора.

Задача 3. Вывести формулу для индуктивности цилиндрического провода длиной l радиусом R, обусловленной потокосцеплением в теле самого провода.
На рисунке показан вид провода с торца.
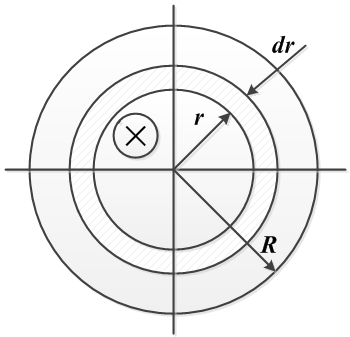
Задача 3. Рисунок. Индуктивность цилиндрического провода
Решение:
Пропустим вдоль провода постоянный ток I. По закону полного тока напряженность поля Н на расстоянии r от оси провода равна току ${I/{{pi}R^2}}{pi}r^2$ , охваченному окружностью радиусом r и деленному на длину этой окружности 2{pi}r : $H={Ir}/{2{pi}R^2}{pi}r^2$ . Индукция $B={{mu}_a}H$ .

Магнитная энергия, запасенная в теле провода вычисляется по формуле:
$W_M=int{0}{R}{{{HB/2}}2{pi}rldr}={{{{mu}_a}{I^2}l}/{16{pi}R^4}}int{0}{R}{{r^3}dr}={{{mu}_a}{I^2}l}/{16{pi}}$ .

Получаем формулу индуктивности цилиндрического провода:
$L={2W_M}/{l^2}={{{mu}_a}l}/{8{pi}}$ .

Ответ: $L={{{mu}_a}l}/{8{pi}}$ — формула индуктивности цилиндрического провода.

Задача 4. Найти токи в схеме.
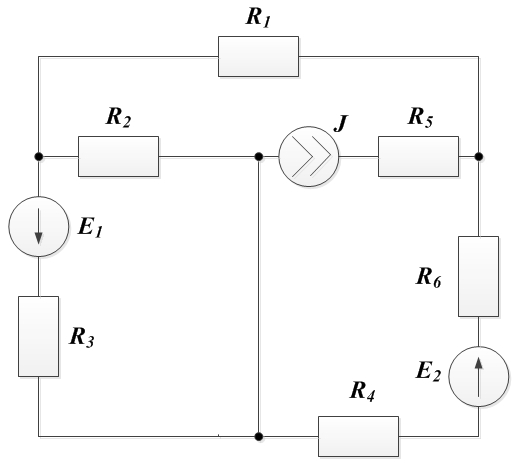
Задача 4. Рисунок 1. Законы Кирхгофа
R₁ = 5 Ом; R₂ = 10 Ом; R₃ = 10 Ом; R₄ = 3 Ом; R₅ = 40 Ом; R₆ = 7 Ом; E₁ = 40 В; E₂ = 10 В; J₁ = 1 A.

Решение:
Расчет цепи ведем по законам Кирхгофа.
Топология.
Определяем общее число ветвей:
p* = 5
Определяем число ветвей с источниками тока:
p_ит = 1.
Определяем число ветвей с неизвестными токами:
p = p* ‐ p_ит = 4.
Находим количество узлов q = 3.
Находим число уравнений, составляемых по первому закону Кирхгофа:
q ‐ 1 = 2.
Находим число уравнений, составляемых по второму закону Кирхгофа:
n = p* — (q — 1) = 2.
Произвольно наносим на схему номера и направления неизвестных токов
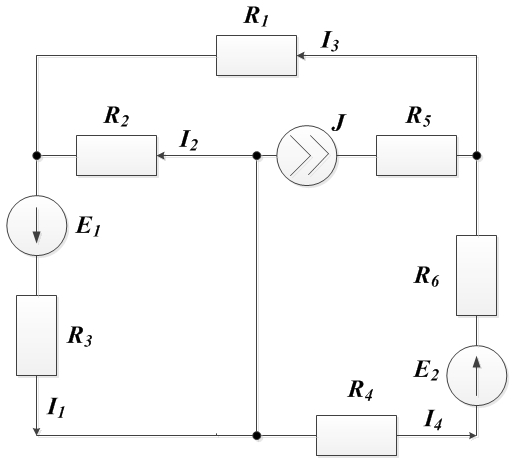
Задача 4. Рисунок 2. Законы Кирхгофа
Произвольно наносим на схему номера узлов:
Задача 4. Рисунок 3. Законы Кирхгофа
Составляем узловые уравнения для произвольно выбранных узлов – для узлов 3 и 1:
I_1-I_2-J-I_4=0
I_2+I_3-I_1=0
Обозначаем на схеме контура и выбираем направления их обхода. Количество обозначаемых контуров равно количеству уравнений, составляемых по второму закону Кирхгофа. При этом ни один из контуров не должен включать в себя ветвь с источником тока
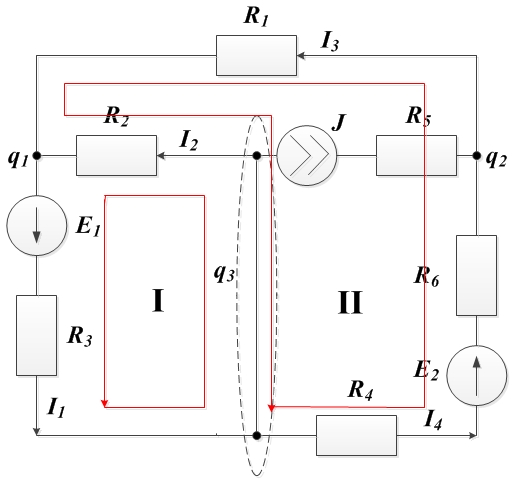
Задача 4. Рисунок 4. Законы Кирхгофа

Составляем контурные уравнения для выбранных контуров:
I_1*R_3+I_2*R_2=E_1
I_3*R_1-I_2*R_2+I_4*R_4+I_4*R_6=E_2

Объединяем составленные уравнения в систему. Известные величины переносим в правую часть уравнений. Удобно, если токи в уравнении стоят по порядку возрастания индексов:
I_1-I_2-I_4=J
-I_1+I_2+I_3=0
I_1*R_3+I_2*R_2=E_1
-I_2*R_2+I_3*R_1+I_4*(R_4+R_6)=E_2

Коэффициенты при искомых токах вносим в матрицу А (левые части уравнений).Заполняем матрицу F, занося в нее правые части уравнений.
$A=(matrix{4}{4}{1 {-1} 0 {-1~} {-1} 1 1 {0~} 10 10 0 {0~} 0 {-10} 5 {10~}});~F=(matrix{4}{1}{J 0 {E_1} {E_2}})$
Решаем полученную систему уравнений с помощью on-line калькулятора (например Matrix calculator).
Полученные токи: I₁ = 3 А; I₂ = 1 А; I₃ = 2 А; I₄ = 1 А.
О том, как решать системы линейных уравнений читайте здесь.

Проверяем правильность решения составлением баланса мощностей.
Подсчитываем мощность, потребляемую резистивными элементами схемы:
P_П= ${I_1}^2*R_3+{I_2}^2*R_2+{I_3}^2*R_1+{I_4}^2*(R_4+R_6)=$
${}=3^2*10+1^2*10+2^2*5+1^2*(3+7)=130$ Вт.

Подсчитываем мощность источников ЭДС. При этом знак минус выбирают, если выбранное направление тока в ветви с источником и стрелка в источнике не совпадают:
$P_E={pm}E*I=E_1*I_1+E_2*I_4=40*3+10*1=130$ Вт.

Подсчитываем мощность источников тока: P_J=J*U_J . Величина U_J неизвестна, ее необходимо определить. Для этого выбирают любой контур, содержащий источник тока, и для этого контура составляется контурное уравнение.
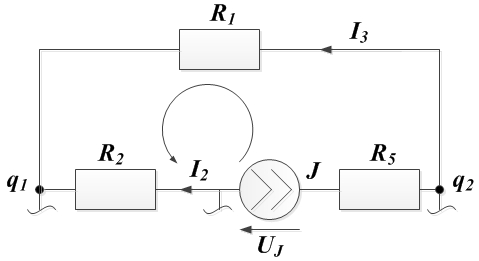
Задача 4. Рисунок 5. Законы Кирхгофа
Направление стрелки напряжения U_J всегда выбирают против тока источника. Далее из этого уравнения, в котором все величины уже известны, можно определить U_J :
I_3*R_1-I_2*R_2-U_J=0
Отсюда
U_J=I_3*R_1-I_2*R_2=10-10=0 Вт.

Таким образом, P_П = P_E. Баланс мощностей соблюден, значит, решение верно.

Ответ: I₁ = 3 А; I₂ = 1 А; I₃ = 2 А; I₄ = 1 А.

Примеры решения задач по физике здесь, решенные задачи из курса физики для школьников, абитуриентов и студентов.

Электронные версии сборников задач по электротехнике

Авербух А.М. Решения задач по неполнофазным режимам и сложным видам коротких замыканий. 1972г.
Авербух А.М. Примеры расчетов неполнофазных режимов и коротких замыканий. 1979г.
Андреев Г.П. Сборник задач и упражнений по теоретическим основам электротехники. 1982г.
Андреев Г.П. Задачник по теоритическим основам электротехники. 1962г.
Беляева Е.Н. Как рассчитать ток короткого замыкания. Издание 2. 1983г.
Бессонов Л.А. Сборник задач по теоретическим основам электротехники. Издание 2. 1980г.
Бессонов Л.А. Сборник задач по теоретическим основам электротехники. 1975г.
Гайах Т. Простейшие электротехнические расчеты. 1968г.
Герасимов В.Г. Сборник задач по электротехнике и основам электроники. 1987г.
Гинзбург С.Г. Методы решения задач по переходным процессам в электрических цепях. 1967г.
Гольдин О.Е. Задачник по курсу теоретических основ электротехники. 1960г.
Гуревич И.В. Основы расчетов радиотехнических цепей. 1975г.
Зайцев И.А. Задачник по теоретическим основам электротехники. Издание 2. 1961г.
Зайцев И.А. Задачник по теоретическим основам электротехнике. Издание 2. 1961г.
Зайчик М.Ю. Сборник задач и упражнений по теоретической электротехнике. 1988г.
Ионкин П.А. Сборник задач и упражнений по общей электротехнике. Издание 2. 1952г.
Ионкин П.А. Сборник задач и упражнений по общей электротехнике. 1955г.
Ионкин П.А. Сборник задач и упражнений по теоретическим основам электротехники. 1982г.
Константинов В.И. Сборник задач по теоретической электротехнике. Издание 5. 1970г.
Константинов В.И. Сборник задач по теоретической электротехнике. 1968г.
Константинов В.И. Сборник задач с решениями по общей электротехнике. 1972г.
Константинов В.И. Сборник задач по теоретической электротехнике.
Куренев С.И. Сборник задач по расчету электрических цепей. 1967г.
Куренев С.И. Сборник задач по расчету электрических цепей. 1967г.
Липатов Д.Н. Вопросы и задачи по электротехнике для программированного обучения. 1973г.
Липатов Д.Н. Вопросы и задачи по электротехнике для программированного обучения. 1984г.
Лосев А.К. Задачник по теории линейных электрических цепей. 1989г.
Миловзорова З.И. Электромагнитная техника в задачах, упражнениях и расчетах. 1975г.
Москалев Л.А. Задачник по электротехнике. Издание 3. 1959г.
Пантюшин В.С. Сборник задач по электротехнике и основам электроники. 1979г.
Пантюшин В.С. Сборник задач по общей электротехнике. 1973г.
Понаморенко В.К. Сборник задач с решениями по общей электротехнике. 1972г.
Раскатов А.И. Задачник по электронике и электрооборудованию. Издание 2. 1962г.
Раскатов А.И. Задачник по электронике и электрооборудованию. Издание 3. 1964г.
Рекус Г.Г. Сборник задач и упражнений по электротехнике и основам электроники. 2001г.
Ульянов С.А. Сборник задач по электромагнитным переходным процессам в электрических системах. 1968г.
Читечян В.И. Электрические машины. Сборник задач. 1988г.
Шебес М.Р. Сборник упражнений и задач по теоретическим основам электротехники. 1962г.
Шебес М.Р. Теория линейных электрических цепей в упражнениях и задачах. Издание 2. 1973г.
Шебес М.Р. Задачник по теории линейных электрических цепей.
Скачать книги можно здесь.

Теоретические основы электротехники — книги по ТОЭ.

Проверить правильность решения практически любой задачи по электротехнике можно при помощи виртуальной лаборатории — Electronics Workbench.

Еще одна программа, которая может быть полезна при решении задач — ТОЭ Super Solver-Circuit magic.

ТОЭ Super Solver-Circuit magic – программа для студентов изучающих теоретические основы электротехники и основы теории цепей. Circuit magic предназначена для создания схем электрических цепей, расчета токов, напряжений, составления балансов мощности, построения и корректировки векторных диаграмм токов и напряжений.

Circuit Magic производит расчет электрических цепей по законам Кирхгофа, методом контурных токов и методом узловых потенциалов. ТОЭ Super Solver-Circuit magic можно использовать в качестве редактора электрических схем и векторных диаграмм.

Для вывода и оформления результатов расчета в состав Circuit Magic включен встроенный текстовый редактор. Скачать Circuit Magic. Посетить сайт программы Circuit Magic.

Поделитесь с друзьями: